codeforces #346 div 2 D. Bicycle Race (思维,计算几何,公式)
题目链接 题意:给出n+1个点,每次由i点到i+1点,每段线段之间保证不同向或者反向,第一个点和最后一个点保证重合。路径围城的封闭图形中间都是水,问有多少个危险点,使得如果在这个点忘记转弯就会掉进水里。
思路:搞了半天没搞出来qaq
From the track description follows that Maria moves the way that the water always located to the right from her, so she could fall into the water only while turning left. To check if the turn is to the left, let's give every Maria's moves directions a number: moving to the north — 0, moving to the west — 1, to the south — 2 and to the east — 3. Then the turn is to the left if and only if the number of direction after performing a turn _dir_ is equal to the number before performing a turn _oldDir_ plus one modulo 4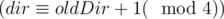 .This solution has complexity O(n).
/* ***********************************************
Author :111qqz
Created Time :2016年03月31日 星期四 01时51分56秒
File Name :code/cf/#346/D.cpp
************************************************ */
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <cmath>
#include <cstdlib>
#include <ctime>
#define fst first
#define sec second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define ms(a,x) memset(a,x,sizeof(a))
typedef long long LL;
#define pi pair < int ,int >
#define MP make_pair
using namespace std;
const double eps = 1E-8;
const int dx4[4]={1,0,0,-1};
const int dy4[4]={0,-1,1,0};
const int inf = 0x3f3f3f3f;
const int N=1005;
int n;
int dir[N];
struct node
{
int x,y;
int getdir( node b)
{
if (x==b.x)
{
if (y>b.y) return 0;
else return 2;
}
else
{
if (x>b.x) return 1;
else return 3;
}
}
}p[N];
int main()
{
#ifndef ONLINE_JUDGE
freopen("code/in.txt","r",stdin);
#endif
cin>>n;
ms(dir,-1);
for ( int i = 1 ; i <= n+1 ; i++) cin>>p[i].x>>p[i].y;
for ( int i = 1 ; i <= n ; i++)
{
dir[i] = p[i].getdir(p[i+1]);
}
int ans = 0 ;
for ( int i = 1 ; i <= n-1 ; i++)
{
if (dir[i]==(dir[i+1]+1)%4) ans++;
}
cout<<ans<<endl;
#ifndef ONLINE_JUDGE
fclose(stdin);
#endif
return 0;
}
以及还有一个O(1)的做法。。太神啦。。。
One can solve this problem in alternative way. Let the answer be equal to _x_ (that means that the number of inner corners of 270 degrees equals _x_, but the number of inner corners of 90 degrees to _n_ - _x_). As soon as the sum of the inner corners' values of polygon of _n_ vertices is equal to 180 × (_n_ - 2), then_x_ × 270 + (_n_ - _x_) × 90 equals to 180 × (_n_ - 2). This leads us to  , being the answer for the problem calculated in _O_(1).